über 170 kostenlose
Prüfungsaufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Lösung Mittlere-Reife-Prüfung 2011 Mathematik I Aufgabe B1
Aufgabe B1.2
(3 Punkte)
Punkte liegen auf der Strecke . Die Winkel haben das Maß mit . Die Punkte sind zusammen mit den Punkten und die Eckpunkte von gleichschenkligen Dreiecken mit der gemeinsamen Basis .
Die Winkel haben das Maß .
Zeichnen Sie das Dreieck für in das Schrägbild zu 1.1 ein.
Für alle Dreiecke gilt: .
Begründen Sie die obere Intervallgrenze.
Die Winkel haben das Maß .
Zeichnen Sie das Dreieck für in das Schrägbild zu 1.1 ein.
Für alle Dreiecke gilt: .
Begründen Sie die obere Intervallgrenze.
Lösung zu Aufgabe B1.2
Skizze
Dreieck für einzeichnen:
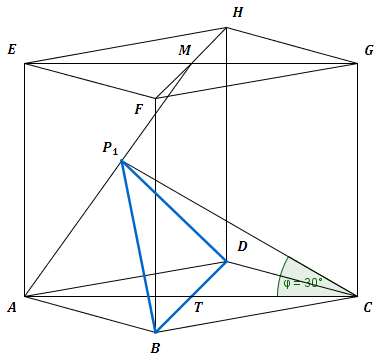
Winkel bestimmen
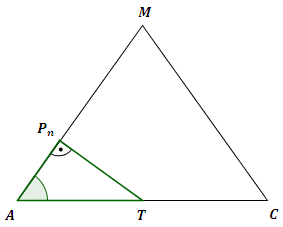
Gesucht ist der größte Wert, den annehmen kann.
ist die Höhe der gleichschenkligen Dreiecke
ist genau dann am größten, wenn die Höhe minimal ist.
ist genau dann minimal, wenn senkrecht auf steht. Für diesen Fall betrachtet man das rechtwinklige Dreieck .
ist die Höhe der gleichschenkligen Dreiecke
ist genau dann am größten, wenn die Höhe minimal ist.
ist genau dann minimal, wenn senkrecht auf steht. Für diesen Fall betrachtet man das rechtwinklige Dreieck .

Im rechtwinkligen Dreieck gilt:
Für diesen kleinsten Wert muss jetzt noch berechnet werden.
Dazu betrachtet man das rechtwinklige Dreieck .
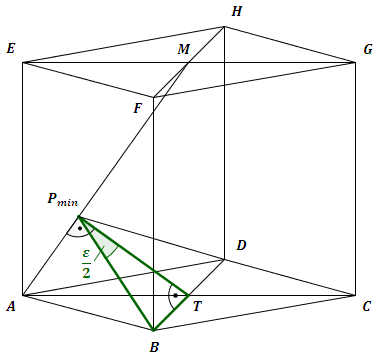
Für diesen kleinsten Wert muss jetzt noch berechnet werden.
Dazu betrachtet man das rechtwinklige Dreieck .

Im rechtwinkligen Dreieck gilt:
Lösungen zu:
Themen dieser Aufgabe:
Feedback:
Du hast einen
Fehler
gefunden oder hast Anregungen zur Internetseite?