Mittlere-Reife-Prüfung 2018 Mathematik Mathematik II Aufgabe A2 Aufgabe 3

über 170 kostenlose

Prüfungsaufgaben

Lösung als Video

und ausformuliert

Alle Lösungen von

erfahrenen Lehrern

Lösung Mittlere-Reife-Prüfung 2018 Mathematik II Aufgabe A2

zur Angabe dieser Mittlere-Reife-Prüfungsaufgabe

Aufgabe A2.3 (3 Punkte)

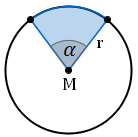
Der Kreis um

E

mit dem Radius

3 cm

schneidet die Strecke

[AE]

im Punkt

P

und die Strecke

[BE]

im Punkt

Q

.
Zeichnen Sie den Kreisbogen

\overset{⌢}{PQ}

in die Zeichnung zu A 2.0 ein.
Berechnen Sie sodann den Flächeninhalt des Kreissektors, der durch die Strecken

[QE]

[EP]

und den Kreisbogen

\overset{⌢}{PQ}

begrenzt wird.

Lösung zu Aufgabe A2.3

Skizze

weitere Mittlere-Reife-Prüfungsaufgaben zu diesem Thema

Einzeichnen

- Beim Punkt

E

einstechen und eine Länge von

3 cm

auf der Strecke

[AE]

antragen. Hier befindet sich der Punkt

P

.

- Der Schnittpunkt der Kreislinie um Punkt

E

mit

r = 3 cm

und der Strecke

[EB]

ergibt Punkt

Q

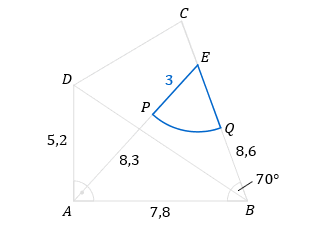
Flächeninhalt einer geometrischen Figur

weitere Mittlere-Reife-Prüfungsaufgaben zu diesem Thema

Gegeben:

\bar{EP} = 3 cm

Gesucht: Flächeninhalt des Kreissekktors

A_{EPQ}

Sinussatz

In jedem Dreieck haben die Quotienten aus der Länge einer Seite und dem Sinuswert ihres Gegenwinkels denselben Wert. Es gilt:

\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ}

Anders formuliert:

\frac{a}{b} = \frac{\sin α}{\sin β}

\frac{a}{c} = \frac{\sin α}{\sin γ}

\frac{b}{c} = \frac{\sin β}{\sin γ}

Im Dreieck

ABE

gilt somit:

\frac{\bar{AB}}{\sin ∡ AEB} = \frac{\bar{BE}}{\sin ∡ BAE} = \frac{\bar{AE}}{\sin ∡ EBA}

\frac{\bar{AB}}{\sin ∡ AEB} = \frac{\bar{AE}}{\sin ∡ EBA}

\frac{7, 8}{\sin ∡ AEB} = \frac{8, 3}{\sin 70^{\circ}}

| \cdot \sin ∡ AEB

7, 8 = \frac{8, 3 \cdot \sin ∡ AEB}{\sin 70^{\circ}}

| \cdot \sin 70^{\circ}

7, 8 \cdot \sin 70^{\circ} = 8, 3 \cdot \sin ∡ AEB

|

: 8, 3

\frac{7, 8 \cdot \sin 70^{\circ}}{8, 3} = \sin ∡ AEB

\Rightarrow

∡ AEB = 62, 0^{\circ}

Nun kann der Flächeninhalt des Kreissektors

A_{EPQ}

berechnet werden:

Flächeninhalt eines Kreissektors

Der Flächeninhalt

A

eines Kreissektors wird gemäß der Formel

A = r^{2} \cdot π \cdot \frac{α}{360^{\circ}}

berechnet.

r^{2} \cdot π

ist der Flächeninhalt des ganzen Kreises.

\frac{α}{360^{\circ}}

gibt den Anteil des Kreissektors am ganzen Kreis an

A_{EPQ} = 3^{2} \cdot π \cdot \frac{62^{\circ}}{360^{\circ}} = 4, 9 {cm}^{2}

Alle Mittlere-Reife-Prüfungsaufgaben

Lösungen zu:

Aufgabe A2.1

Aufgabe A2.2

Aufgabe A2.3

Lösung als Video:

Themen dieser Aufgabe:

Skizze

Flächeninhalt einer geometrischen Figur

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!

Realschulrep.de bei
Facebook