über 170 kostenlose
Prüfungsaufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
AB SOFORT: KEIN LOGIN mehr erforderlich - alle Lösungen zu den Prüfungsaufgaben sind frei zugänglich.
 
Mittlere-Reife-Prüfung 2009 Mathematik I Aufgabe B2
Aufgabe B2.

Die nebenstehende Skizze zeigt ein Schrägbild des geraden Prismas A B C D E F , dessen Grundfläche das gleichschenklige Dreieck A B C mit der Basis [ A B ] und der Höhe [ M C ] , ist.
Es gilt: A B ¯ = 5 cm ; A 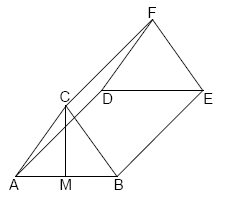D ¯ = 12 cm ; M C ¯ = 4 cm.

Aufgabe B2.1  (2 Punkte)

Zeichnen Sie das Schrägbild des Prismas A B C D E F , wobei die Kante [ A B ] auf der Schrägbildachse liegen soll (Lage des Prismas wie in der Skizze zu 2.0 dargestellt).
Für die Zeichnung gilt: q = 1 2 ; ω = 45 ∘ .
Berechnen Sie sodann das Maß des Winkels C B A .
[Ergebnis: ∡ C B A = 57 , 99 ∘ ]

Aufgabe B2.2  (1 Punkt)

Punkte G n ∈ [ B C ] und Punkte H n ∈ [ E F ] sind zusammen mit den Punkten A und D die Eckpunkte von Rechtecken A G n H n D . Die Winkel B A G n haben das Maß φ mit φ ∈ [ 0 ∘ ; 57 , 99 ∘ ] .
Zeichnen Sie das Rechteck A G 1 H 1 D für B G 1 ¯ = 1 4 in das Schrägbild zu 2.1 ein.

Aufgabe B2.3  (5 Punkte)

Berechnen Sie den Flächeninhalt A der Rechtecke A G n H n D in Abhängigkeit von φ . Ermitteln Sie sodann den minimalen und den maximalen Flächeninhalt mit dem jeweils zugehörigen Winkelmaß φ .
[Teilergebnis: A G n ¯ ( φ ) = 4 , 24 sin ( φ + 57 , 99 ∘ ) cm]

Aufgabe B2.4  (3 Punkte)

Die Rechtecke A G 2 H 2 D und A G 3 H 3 D haben jeweils den Flächeninhalt 53 cm 2 . Berechnen Sie die zugehörigen Winkelmaße φ .

Aufgabe B2.5  (2 Punkte)

Ermitteln Sie rechnerisch das Volumen V der Prismen A B G n D E H n in Abhängigkeit von φ .
[Ergebnis: V ( φ ) = 127 , 20 ⋅ sin φ sin ( φ + 57 , 99 ∘ ) cm 3 ]

Aufgabe B2.6  (4 Punkte)

Das Volumen des Prismas A B G 4 D E H 4 beträgt 20 % des Volumens des Prismas A B C D E F .
Berechnen Sie das zugehörige Winkelmaß φ .

Lösung als Video:
video

 
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?