über 170 kostenlose
Prüfungsaufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
AB SOFORT: KEIN LOGIN mehr erforderlich - alle Lösungen zu den Prüfungsaufgaben sind frei zugänglich.
 
Mittlere-Reife-Prüfung 2012 Mathematik I Aufgabe B2
Aufgabe B2.

Die nebenstehende Skizze zeigt ein Schrägbild des geraden
Prismas A B C D E F , dessen Grundfläche das rechtwinklige
Dreieck A B C mit den Katheten [ A B ] und [ A C ] ist.
Es gilt: A B ¯ = A D ¯ = 6 cm; A C ¯ = 8 cm.

Runden Sie im Folgenden auf zwei Stellen nach dem
Komma.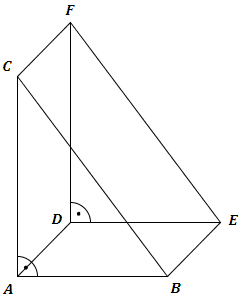

Aufgabe B2.1  (4 Punkte)

Zeichnen Sie das Schrägbild des Prismas A B C D E F , wobei die Kante [ A B ] auf der Schrägbildachse liegen soll (Lage des Prismas wie in der Skizze zu 2.0 dargestellt).
Für die Zeichnung gilt: q = 1 2 ; ω = 45 ∘ .
Berechnen Sie sodann die Länge der Strecke [ F E ] und das Maß des Winkels A F E .
[Ergebnis: F E ¯ = 10 cm; ∡ A F E = 50 , 21 ∘ ]

Aufgabe B2.2  (3 Punkte)

Punkte Q n liegen auf der Strecke [ F E ] . Die Winkel F Q n A haben das Maß φ mit φ ∈ [ 64 , 90 ∘ ; 129 , 79 ∘ [ . Die Punkte Q n sind zusammen mit den Punkten A und F Eckpunkte von Dreiecken A Q n F .
Zeichnen Sie das Dreieck A Q 1 F für F Q 1 ¯ = 4 cm in das Schrägbild zu 2.1 ein.
Begründen Sie sodann die Intervallgrenzen für φ .

Aufgabe B2.3  (2 Punkte)

Berechnen Sie die Länge der Strecken [ F Q n ] in Abhängigkeit von φ .
[Ergebnis: F Q n ¯ ( φ ) = 10 ⋅ sin ( 50 , 21 ∘ + φ ) sin φ cm]

Aufgabe B2.4  (3 Punkte)

Die Punkte Q n sind die Spitzen von Pyramiden A D F Q n mit der Grundfläche A D F und den Höhen [ P n Q n ] . Die Punkte P n liegen auf der Strecke [ D F ] .
Zeichnen Sie die Pyramide A D F Q 1 und die Höhe [ P 1 Q 1 ] in das Schrägbild zu 2.1 ein. Ermitteln Sie sodann durch Rechnung das Volumen V der Pyramiden A D F Q n in Abhängigkeit von φ .
[Ergebnis: V ( φ ) = 48 ⋅ sin ( 50 , 21 ∘ + φ ) sin φ cm³]

Aufgabe B2.5  (3 Punkte)

Das Volumen der Pyramide A D F Q 2 ist um 70 % kleiner als das Volumen des Prismas A B C D E F . Berechnen Sie das zugehörige Winkelmaß φ .

Aufgabe B2.6  (2 Punkte)

Die Höhe der Pyramide A B E D Q 3 mit der Grundfläche A B E D hat das gleiche Maß wie die Höhe der Pyramide A D F Q 3 . Begründen Sie, dass das Volumen der Pyramide A B E D Q 3 1 , 5 mal so groß ist wie das Volumen der Pyramide A D F Q 3 .

Lösung als Video:
video

 
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?